Analysis of Algorithms, Complexity
K08 Δομές Δεδομένων και Τεχνικές Προγραμματισμού
Κώστας Χατζηκοκολάκης
Outline
- How can we measure and compare algorithms meaningfully?
- an algorithm will run at different speeds on different computers
- $O$ notation.
- Complexity types.
- Worst-case vs average-case
- Real-time vs amortized-time
Selection sort algorithm
// Ταξινομεί τον πίνακα array μεγέθους size
void selection_sort(int array[], int size) {
// Βρίσκουμε το μικρότερο στοιχείο του πίνακα, το τοποθετούμε στη θέση 0,
// και συνεχίζουμε με τον ίδιο τρόπο στον υπόλοιπο πίνακα.
for (int i = 0; i < size; i++) {
// βρίσκουμε το μικρότερο στοιχείο από αυτά σε θέσεις >= i
int min_position = i;
for (int j = i; j < size; j++)
if (array[j] < array[min_position])
min_position = j;
// swap των στοιχείων i και min_position
int temp = array[i];
array[i] = array[min_position];
a[min_position] = temp;
}
}
Running Time
- Array of 2000 integers
- Computers A, B, …, E are progressively faster.
- The algorithm runs faster on faster computers.
| Computer | Time (secs) |
|---|---|
| Computer A | 51.915 |
| Computer B | 11.508 |
| Computer C | 2.382 |
| Computer D | 0.431 |
| Computer E | 0.087 |
More Measurements
- What about different programming languages?
- Or different compilers?
- Can we say whether algorithm A is better than B?
A more meaningful criterion
- Algorithms consume resources: e.g. time and space
- In some fashion that depends on the size of the problem solved
- the bigger the size, the more resources an algorithm consumes
- We usually use $n$ to denote the size of the problem
- the length of a list that is searched
- the number of items in an array that is sorted
- etc
selection_sort running time
In msecs, on two types of computers
| Array Size | Home Computer | Desktop Computer |
|---|---|---|
| 125 | 12.5 | 2.8 |
| 250 | 49.3 | 11.0 |
| 500 | 195.8 | 43.4 |
| 1000 | 780.3 | 172.9 |
| 2000 | 3114.9 | 690.5 |
Curves of the running times
If we plot these numbers, they lie on the following two curves:
- $ f_1(n) = 0.0007772n^2 + 0.00305n + 0.001$
- $ f_2(n) = 0.0001724n^2 + 0.00040n + 0.100$
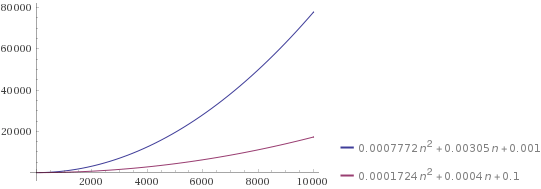
Discussion
-
The curves have the quadratic form $f(n) = an^2 + bn + c$
- difference: they have different constants $a,b,c$
-
Different computer / programming language / compiler:
- the curve that we get will be of the same form!
-
The exact numbers change, but the shape of the curve stays the same.
Complexity classes, $O$-notation
-
We say that an algorithm belongs to a complexity class
-
A class is denoted by $O(g(n))$
- $g(n)$ gives the running time as a function of the size $n$
- it describes the shape of the running time curve
-
For
selection_sortthe time complexity is $O(n^2)$- take the dominant term of the expression $an^2+bn+c$
- throw away the constant coefficient $a$
Why only the dominant term?
$f(n) = an^2 + bn + c$
with $a = 0.0001724, b = 0.0004$ and $c = 0.1$.
| $n$ | $f(n)$ | $an^2$ | $n^2$ term as % of total |
|---|---|---|---|
| 125 | 2.8 | 2.7 | 94.7 |
| 250 | 11.0 | 10.8 | 98.2 |
| 500 | 43.4 | 43.1 | 99.3 |
| 1000 | 172.9 | 172.4 | 99.7 |
| 2000 | 690.5 | 689.6 | 99.9 |
Why only the dominant term?
- The lesser term $bn+c$ contributes very little
- even though $b,c$ are much larger than $a$
- Thus we can ignore this lesser term
- Also: we ignore the constant $a$ in $an^2$
- It can be thought of as the “time of a single step”
- It depends on the computer / compiler / etc
- We are only interested in the shape of the curve
Common complexity classes
| $O$-notation | Adjective Name |
|---|---|
| $O(1)$ | Constant |
| $O(\log n)$ | Logarithmic |
| $O(n)$ | Linear |
| $O(n \log n)$ | Quasi-linear |
| $O(n^2)$ | Quadratic |
| $O(n^3)$ | Cubic |
| $O(2^n)$ | Exponential |
| $O(10^n)$ | Exponential |
| $O(2^{2^n})$ | Doubly exponential |
Sample running times for each class
Assume 1 step = 1 μsec.
| $g(n)$ | $n=2$ | $n=16$ | $n=256$ | $n=1024$ |
|---|---|---|---|---|
| 1 | 1 μsec | 1 μsec | 1 μsec | 1 μsec |
| $\log n$ | 1 μsec | 4 μsec | 8 μsec | 10 μsec |
| $n$ | 2 μsec | 16 μsec | 256 μsec | 1.02 ms |
| $n \log n$ | 2 μsec | 64 μsec | 2.05 ms | 10.2 ms |
| $n^2$ | 4 μsec | 25.6 μsec | 65.5 ms | 1.05 |
| $n^3$ | 8 μsec | 4.1 ms | 16.8 ms | 17.9 min |
| $2^n$ | 4 μsec | 65.5 ms | $10^{63}$ years | $10^{297}$ years |
The largest problem we can solve in time T
Assume 1 step = 1 μsec.
| $g(n)$ | T = 1 min | T = 1hr |
|---|---|---|
| $n$ | $6 \times 10^7$ | $3.6 \times 10^9$ |
| $n\log n$ | $2.8 \times 10^6$ | $1.3 \times 10^8$ |
| $n^2$ | $7.75 \times 10^3$ | $6.0 \times 10^4$ |
| $n^3$ | $3.91 \times 10^2$ | $1.53 \times 10^3$ |
| $2^n$ | $25$ | $31$ |
| $10^n$ | $7$ | $9$ |
Complexity of well-known algorithms
| Sequential searching of an array | $O(n)$ |
| Binary searching of a sorted array | $O(\log n)$ |
| Hashing (under certain conditions) | $O(1)$ |
| Searching using binary search trees | $O(\log n)$ |
| Selection sort, Insertion sort | $O(n^2)$ |
| Quick sort, Heap sort, Merge sort | $O(n \log n)$ |
| Multiplying two square x matrices | $O(n^3)$ |
| Traveling salesman, graph coloring | $O(2^n)$ |
Formal definition of $O$-notation
$f(n)$ is the function giving the actual time of the algorithm.
We say that $f(n)$ is $O(g(n))$ iff
- there exist two positive constants $K$ and $n_0$
- such that $|f(n)| \leq K|g(n)| \quad \forall n \geq n_0$.
We will not focus on the formal definition in this course.
Intuition
-
An algorithm runs in time $O(g(n))$ iff it finishes in at most $g(n)$ steps.
-
A “step” is anything that takes constant time
- a basic operation, eg
a = b + 3 - a comparison, eg
if(a == 4) - etc
- a basic operation, eg
-
Typical way to compute this
- find an expression $f(n)$ giving the exact number of steps
(or an upper bound) - find $g(n)$ by removing the lesser terms and coefficients
(justified by the formal definition)
- find an expression $f(n)$ giving the exact number of steps
Example
- An algorithm takes $f(n)$ number of steps, where
- $f(n) = 3 + 6 + 9 + \dots + 3n $
- We will show that the algorithm runs in $O(n^2)$ steps.
- First find a closed form for $f(n)$:
- $f(n) = 3 (1+2+\dots+n) = 3 \frac{n(n+1)}{2} = \frac{3}{2} n^2 + \frac{3}{2}n$
- Throw away
- the lesser term $\frac{3}{2}n$
- and the coefficient $\frac{3}{2}$
- We get $O(n^2)$
Scale of strength for $O$-notation
To determine the dominant term and the lesser terms:
$$O(1) < O(\log n) < O(n) < O(n^2) < O(n^3) < O(2^n) < O(10^n)$$
Example:
- $O(6n^3-15n^2+3n \log n ) = O(6n^3) = O(n^3)$
Ignoring bases of logarithms
- When we use $O$-notation, we can ignore the bases of logarithms
- assume that all logarithms are in base 2.
- Changing base involves multiplying by a constant coefficient
- ignored by then $O$-notation
- For example, $\log_{10} n = \frac{\log n}{\log 10}$ . Notice now that $\frac{1}{\log 10} $ is a constant.
$O(1)$
- It is easy to see why the $O(1)$ notation is the right one for constant time
- Constant time means that the algorithm finishes in $k$ steps
- $O(k)$ is the same as $O(1)$, constants are ignored
Caveat 1
- $O$-complexity talks about the behaviour for large values of $n$
- this is why we ignore lesser terms!
- For small sizes a “bad” algorithm might be faster than a “good” one
- We can test the algorithms experimentally to choose the best one
Caveat 2
- $O(g(n))$ complexity is an upper bound
- the algorithm finishes in at most $g(n)$ steps
- Comparing algorithms can be misleading!
- item A costs at most 10 euros
- item B costs at most 5000 euros
- which one is cheaper?
- Programmers often say $O(g(n))$ but mean $\Theta(g(n))$
- finishes in “exactly” $g(n)$ steps
- we won't use $\Theta$ but keep this in mind
Types of complexities
-
Depending on the data
- Worst-case vs Average-case
-
Depending on the number of executions
- Real-time vs amortized-time
Worst-case vs Average-case
-
Say we want to sort an array, which values are stored in the array?
-
Worst-case: take the worst possible values
-
Average-case: average wrt to all possible values
-
Eg. quicksort
- worst-case: $O(n^2)$ (when data are already sorted)
- average-case: $O(n\log n)$
Real-time vs amortized-time
-
How many times do we run the algorithm?
-
Real-time: just once
- $n$ is the size of the problem
-
Armortized-time: multiple times
- take the average wrt all execution (not wrt the values!)
- $n$ is the number of executions
-
Example: Dynamic array! (we will see it soon)
Some algorithms and their complexity
We will analyze the following algorithms
- Sequential search
- Selection sort
- Recursive selection sort
Sequential search
// Αναζητά τον ακέραιο target στον πίνακα target. Επιστρέφει τη θέση
// του στοιχείου αν βρεθεί, διαφορετικά -1
int sequential_search(int target, int array[], int size) {
for (int i = 0; i < size; i++)
if (array[i] == target)
return i;
return -1;
}
- The steps to locate
targetdepends on its position inarray- if
targetis inarray[0], then we need only one step - if
targetis inarray[i-1], then we need $i$ steps
- if
Complexity analysis
Worst case
- This is when
targetis inarray[size-1] - The algorithm needs $n$ steps
- So its complexity is $O(n)$
Complexity analysis
Average case
-
Assume that we always search for a
targetthat exists inarray -
If
target == array[i-1]then we need $i$ steps -
Average wrt all possible positions $i$ (all are equally likely) $$\textstyle \textrm{Average} = \frac{1+\ldots+n}{n} = \frac{ \frac{n(n+1)}{2} }{n} = \frac{n}{2} + \frac{1}{2}$$
-
Therefore the average is $O(n)$
- Same if we consider
targets that don't exist inarray
- Same if we consider
Selection sort algorithm
// Ταξινομεί τον πίνακα array μεγέθους size
void selection_sort(int array[], int size) {
// Βρίσκουμε το μικρότερο στοιχείο του πίνακα, το τοποθετούμε στη θέση 0,
// και συνεχίζουμε με τον ίδιο τρόπο στον υπόλοιπο πίνακα.
for (int i = 0; i < size; i++) {
// βρίσκουμε το μικρότερο στοιχείο από αυτά σε θέσεις >= i
int min_position = i;
for (int j = i; j < size; j++)
if (array[j] < array[min_position])
min_position = j;
// swap των στοιχείων i και min_position
int temp = array[i];
array[i] = array[min_position];
a[min_position] = temp;
}
}
Complexity analysis of selection_sort
- Inner
for- its body is constant: 1 step
- $n - i$ repetitions ($n$ =
size, $i = $current value ofi) - so the whole loop takes $n-i$ steps
- Outer
for:- its body takes $n-i$ steps
- +1 for the constant swapping part (ignored compared to $n-i$)
- first execution: $n$ steps, second: $n-1$ steps, etc
- Total: $n + \ldots + 1 = \frac{n(n+1)}{2}$ steps
- its body takes $n-i$ steps
- So the time complexity of the algorithm is $O(n^2)$
Recursive selection_sort
Auxiliary functions
// Βρίσκει τη θέση του ελάχιστου στοιχείου στον πίνακα array
int find_min_position(int array[], int size) {
int min_position = 0;
for (int i = 1; i < size; i++)
if (array[i] < array[min_position])
min_position = i;
return min_position
}
// Ανταλλάσει τα στοιχεία a,b του πίνακα array
void swap (int array[], int a, int b) {
int temp = array[a];
array[a] = array[b];
array[b] = temp;
}
Recursive selection_sort
Elegant recursive version of the algorithm
// Ταξινομεί τον πίνακα array μεγέθους size
void selection_sort(int array[], int size) {
// Με λιγότερα από 2 στοιχεία δεν έχουμε τίποτα να κάνουμε
if (size < 2)
return;
// Τοποθετούμε το ελάχιστο στοιχείο στην αρχή
swap(array, 0, find_min_position(array, size));
// Ταξινομούμε τον υπόλοιπο πίνακα
selection_sort(&array[1], size - 1);
}
Analysis of recursive selection_sort
- How many steps does
selection_sorttake?- Let $g(n)$ denote that number
- $g(0) = g(1) = 1$ (nothing to do)
- For $n > 1$
selection_sortcalls:find_min_position: $n$ stepsswap: 1 step (ignored compared to $n$)selection_sort: $g(n-1)$ steps
So $g(n) = \begin{cases} n + g(n -1) & n > 1 \\ 1 &n \le 1 \end{cases}$
Analysis of recursive selection_sort
This is a recurrence relation, we can solve it by unrolling:
$$ \begin{aligned} g(n) &= n + g(n -1) \\ &= n + (n-1) + g(n-2) \\ &= n + (n-1) + (n-2) + g(n-3) \\ &\ldots \\ &= n + \ldots + 1 \\ &= \frac{n(n+1)}{2} \end{aligned} $$ So again we get complexity $O(n^2)$
ADTList using Linked Lists
What is the worst case complexity of each operation?
list_insert_nextlist_remove_nextlist_nextlist_lastlist_find
Readings
- T. A. Standish. Data Structures, Algorithms and Software Principles in C, Chapter 6.
- Robert Sedgewick. Αλγόριθμοι σε C, Κεφ. 2.